In the photographic community, the common perception is that the exposition scale is symmetrical. The perception dates back to Adams: the Zone V is in the middle of the range, with 5 zones above and below it, top and bottom being symmetrical: there are 2 zones each way containing details, then one more each way with traces of textures, with the final two (one each way) which are respectively completely void white and solid black. The 2x (1eV) changes in brightness correspond to the transition between the zones.
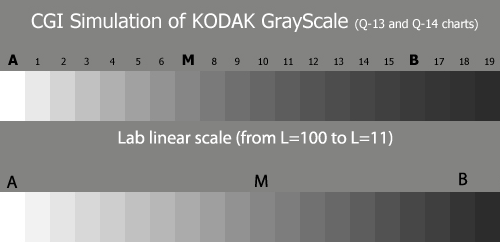 The photographic zone step wedge is not visually (perceptually) even. For instance in the Kodak Q13 grey wedge (the top scale on the image to the left), where the distance between the two neighboring patches is 1/3 eV, we can clearly see that in the lighter part, this distance between the patches seems visually large, and in shadows visually small, as if the steps are compressed. The Q13 wedge encompasses Zones I through VII, although not representing the brightest part (further on, we will see that they cannot be represented at all by an evenly distributed wedge).
The photographic zone step wedge is not visually (perceptually) even. For instance in the Kodak Q13 grey wedge (the top scale on the image to the left), where the distance between the two neighboring patches is 1/3 eV, we can clearly see that in the lighter part, this distance between the patches seems visually large, and in shadows visually small, as if the steps are compressed. The Q13 wedge encompasses Zones I through VII, although not representing the brightest part (further on, we will see that they cannot be represented at all by an evenly distributed wedge).
On the same image, a wedge with the equal steps on L (L is the brightness axis in the Lab color system), is provided for comparison. Visually, the scale is much more even, based on the value of the step, and the standard grey, (patch M in both scales) is located exactly in the middle, contrary to Q13
The middle tone and the dynamic range
The best place for middle tones (Zone V as per Adams) on the printout is specifically the middle tone (L=50 in Lab terms). In that brightness area, the details are perceived the best, which is easily seen after tweaking any photograph in Photoshop.
In the Lab space, the maximum value L=100 corresponds to the highest brightness of the image (the point to which the eye adapts, using it as a reference white), whereas L=50 always corresponds to the brightness, which is 5.5 times smaller. Thus, there are 5 eV steps from the half-tones (Zone V) to the maximum whites (Zone X), and only 2.45 eV steps (2^2.45=5.5) on the output device, regardless of its type. The compression problem was automatically solved for Adams because he used silver-halide photographic paper: the upper 3 zones were compressed to the density range of about 0.3D due to the shoulder of the characteristic curve. Things are a little harder for the digital photographer, since there is no automatic compression of highlights.
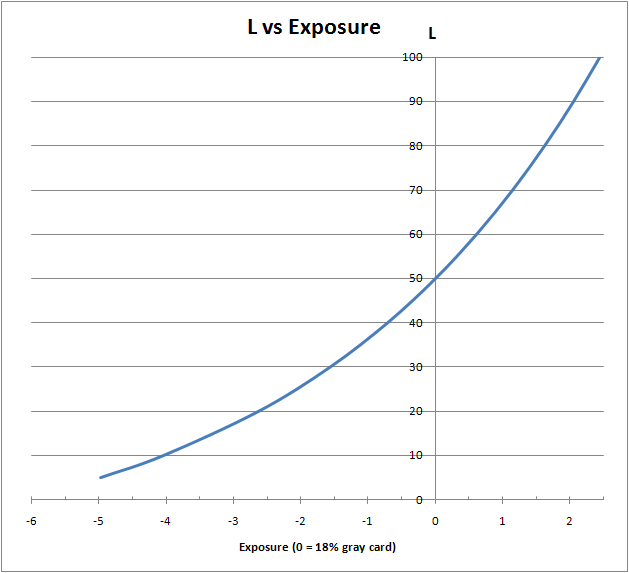 The graph to the left demonstrates the relationship between the value of L (on the output device) and the steps of exposure. It is assumed, that the brightnesses of the scene are reproduced linearly, and the middle tone of the scene (18% grey) is recorded as the middle tone on the print (L=50). From the graph we can tell that:
The graph to the left demonstrates the relationship between the value of L (on the output device) and the steps of exposure. It is assumed, that the brightnesses of the scene are reproduced linearly, and the middle tone of the scene (18% grey) is recorded as the middle tone on the print (L=50). From the graph we can tell that:
-
the space in highlights is very small: only 2.5 eV. That is not a limitation of the output device (the paper, or the monitor), but a trait of the human vision: as soon as we have adapted to the white point (maximum brightness), we can perceive the details best in the area that is 5.5 times less bright.
In the practice of digital photography, the most adequate to vision traits in terms of brightness perception is Lab color space, which is especially constructed with the vision characteristics taken into account, in order to be perceptually even. Even though the Lab space is not used for editing, it is used as an inner working space for Photoshop, as well as a number of other programs. - The space in shadows is a stretched notion. In the best case scenario (a good monitor, which does not limit us in the shadow area), we can hope to save the visibility of something other than the abstract dark blotches all the way to the level of L=10, which corresponds to 4eV down from the middle grey . While printing on paper, the limitation starts at about the L=20 level, or 2.5 eV down from the middle grey (which is now without quotations).
The above-shown graph repeats the Central Exposure column from Iliah Borg s article, except the numbers in the table did not impact the author of this article as much as the graph did.
We should also note that we have not yet pronounced the catch phrases dynamic range or photographic latitude. Everything written above related only to the reproduction of the result: an optimal (in terms of perception) contrast range is at best 1:100 on a monitor (the brightness range of a monitor can be much higher, but then the shadow area will not be used well enough), but could be only as low as 1:32 on some mid-quality paper. Consequently, the brighter part of the resulting image is not reproduced in details and gradations, whereas the dark, even if reproduced is not really perceived by the viewer.
The phenomenon of the optical contrast of the image has been long known to artists and cameramen. Sadly, in photographic texts on the internet, that notion is dealt with rarely, with the dynamic range discussed much more often. Nevertheless, a book by Valentin Zheleznyakov Color and Contrast (in Russian) is available online, a work we direct the Russian-speaking readers towards. Zheleznyakov is the one who employed the term optimal visual contrast. In two words, this phenomenon leads to the above-mentioned: the optimal contrast of the image lies in the range 1:40-1:60, and with bigger contrasts, a loss of details, as well as the loss of the fine gradations in highlights or shadows or both happens. Obviously we are talking about the image, which has to be perceived as one sensation, through static, simultaneous contrast (that does not include visually dissecting the image into separate smaller parts where re-adaptation of the eye occurs, and which is dynamic, non-simultaneous contrast).
Thus we have arrived to the following thesis :
- the middle tone of the actual scene has to be reproduced as the same middle tone.
- the useful range of contrast on the output device is at best 1:100, and is often much less.
- the useful range of the print (or the monitor) is much less limited by the capabilities of the output equipment then by the traits of the human vision, and those are not easily widened (it takes ages for human vision to start perceiving 1eV more of simultaneous contrast).
The first thesis is of course not a dogma. A European face is lighter than middle grey, but is often exposed and printed as a main object, thus giving an extra 1eV in highlights. That is not mentioning high-key and low-key images. Nevertheless, in most cases we want to see the middle tone of the scene positioned in the area of the middle tone of the reproduction, which is what we will be discussing further on.
Now lets talk about digital cameras. Their light sensitive element is linear, thus the 18%-grey results in the 18% signal. In other words, 82% of the levels the camera records correspond to the lighter zones, including about a half of the halftones, whereas the remaining 18% are left for the shadows and the other half of the halftones. On dSLRs with a 12 bit ADC (analog to digital converter, which, until very recently, were the majority), the shadows get about 700 levels, which is more than enough for further editing.
Obviously, the optimum distribution of the number of levels would be 2500:1500 or 2250:1750, since there is 50 L units for lights, and 30-40 for shadows, but the current technology does not leave us a choice.
Nevertheless, the formal dynamic range of the modern DSLR is usually more than 5-7 eV, and the typical landscape or street scene has usually more than 2.5 eV from the middle to the highlights (including the level of white higher than Zone VIII), this making the photographer want to place the scene in the range of the sensor. For the above-mentioned street and landscape scenes, that means 2-3 eV of underexposure for the middle tones relative to the optimum exposition.
As a result, the shadows and the halftones receive 90-180 levels, and accounting for the underexposure of the red channel in the daylight of about 1-1.5 eV (relative to the green), the red can remain with only 40-50 levels, which is definitely not enough for returning the halftones into the target key values without noise, posteration, and other artifacts.
For sensors with a smaller dynamic range that effect is even more destructive. An attempt to place 7-8 eV of a typical scene (as measured by a spotmeter) into the range of the transparency film, often results in underexposure of the halftones of about 1-1.5 eV, which is fatal for the given media. As a result, a contradiction occurs, when the metering of the scene brightness range and its correct placement in the latitude of the photographic material lead to a much worse result, than a mere centerweighed metering of the entire field of the shot.
Furthermore, the latest generation digital camera, featuring a 14- bit ADC, handle an underexposure of 2-3 eV well, at least on the minimal sensitivity settings (actually, base ISO is a better term here). Also, the author s attempt to illustrate the given problem on a murky day in Moscow with the use of such a camera (the range of brightnesses in the scene was within 8 eV) yielded only small, yet visible differences in the reproduction of the shades of the leaves. The camera of an earlier generation behaved much worse in the same conditions.
All of the above-mentioned does not relate to the Fuji S5 camera: the second set of sensors in the camera allows 3-4 eV more in highlights with proper processing, which is enough for the majority of the practical uses.
Practical conclusions
There is a harsh trade-off, while shooting with a digital camera: the shift of the exposure for preserving the details (and sometimes even gradations) in the highlights results in a significantly worse reproduction of the halftones and shadows. This is how the digital camera differs from a film, where the exposure within the limits of a linear part of the characteristic curve of the film can be shifted rather safely.
The possible level of such a trade-off depends on the noise level as well as on the level of imbalance of sensitivities of the channels, and has to be determined by the owner of the camera, basing on the acceptable level of the artifacts in shadows and halftones. This level will vary for different models of cameras and different settings of sensitivities, and the level of acceptability depends, besides everything else on the final size of the print.
We can treat the dSLR as an improved transparency and expose it in a similar manner: allowing just 2.5 eV above the middle grey. Halftones will already be on their place, and there will be almost no need to pull out the shadows. Obviously, there is no such blooming on a transparency, but it is the sources of light which cause the blooming on modern digital cameras, and this effect cannot be avoided through any rational exposure correction. Of course, in many cases, one will have to take measures in order to lower the contrast: lighten the foreground, wait until a change of lighting (for instance, when the sun goes behind the clouds), or use filters. Still, for people that shoot transparencies, this way is ordinary, since it has been used for decades, and yields excellent results.
One more potentially correct way of shooting is hinted at by the Fuji S5: one shot is taken on the target , the second, with an underexposure of 2-3 eV, whereas the final result is achieved through the borrowing of groups of pixels from the underexposed shot into the clipped areas of the properly exposed one. A somewhat widespread program allowing to do that for any given camera is unknown to the author, but this is one of the possible parts of the application of programming efforts. Basically, this is an analog of superimposing the sky a technique which has long been used by film photographers. It is important to note that we are not talking about mixing properly exposed pixels with underexposed (or overexposed) ones, we are talking specifically about the replacement of whole areas of the image.
The HDR technique followed by tonemapping is often used for blending shots taken with different exposures. This method has a number of deficiencies, part of which are an integral property of the method, and some just happen to be often occurring:
- While composing HDR values of a pixel form 12-14 bit raw data, the values used are not only the optimally-exposed variations of the pixel, but also the over/underexposed. As a result, the input of noise (coming from the underexposed pixels) and the nonlinearity of the sensor in the area of high values (from pixels close to overexposure) turns out to be pretty large, which leads to noticeable amount of noise and artifacts on the image.
- Simple tonemapping, which does not increase the local contrast, often results in flat and bland images, thus HDR shooters use various techniques which increase the local contrast. The noise component will also be increased with the increase of the local contrast, which leads to the appearance of dirty hues, which we see regularly on HDR shots.
- The techniques of increasing the local contrast are frequently used in the highlights and shadows of the image, where there is no place for details, since the eye does not see them in a real scene. The resulting images look very artificial and can be easily distinguished from the overall mass even by an untrained viewer, who does not know about HDR techniques. As a result, HDR photography became a separate genre, with the technical side having the most value, similar to what has happened to cross-processing in the past.
Finally, I would like to (translated) quote Zheleznyakov s book (this is a commentary to the table, where the scene contrasts appearing in real life are listed):
however, one of the widespread misconceptions is the assumption that literally all objects listed in the table (including the most contrast ones) can be effortlessly perceived by our vision, but not by a film or video camera. This is only partially correct, because the most contrasty objects are perceived by us only after a whole series of singular acts of vision on different levels of adaptation of each subsequent retinal image, where the sensitivity of the eye and the size of the pupil constantly changes, and where the level of white (thus, also the corresponding to it value of black) is constantly and automatically changed

Comments
Roger W. Hicks writes: The
Roger W. Hicks writes:
The darkest black achievable with a top-flight black and white paper, optimally processed, reflects about 1/200 as much light as the pure, paper-base white: a brightness range of 200:1. Few prints will achieve this: a more realistic brightness range is between 100:1 and 125:1. What is more, there is a difference between the total range -- the purest white and deepest black -- and the dynamic range, within which there is texture and detail. This is very unlikely to exceed 100:1, and may well be more like 64:1.
(http://www.rogerandfrances.com/photoschool/ps%20subject%20brightness%20r...)
--
Iliah Borg